YY分享

1. 功能 

用N点复序列快速傅立叶变换来计算2N点的实序列离散傅立叶变换。

2. 方法简介

3. 算法r1fft.h

#ifndef R1FFT_H_
#define R1FFT_H_
 
/*形参介绍：
 * x——双精度实型一位数组，长度为n。
 * 开始时存放要变换的实数据，最后存放变换结果的前n/2+1个值，
 * 其存储顺序为[Re(0),Re(1),...Re[n/2],Im(n/2-1),...,Im(1)],
 * 其中Re(0)=X(0),Re(n/2)=X(n/2)，根据共轭对称性，很容易写出后半部分的值。
 * n——整型变量，数据长度，必须是2的整数次幂.
 */
#include "fft.h"
 
void r1fft( double x[], int n);
 
void r1fft( double x[], int n)
{
    int i,n1;
    double a,c,e,s,fr,fi,gr,gi,*f,*g;
    f=malloc(n/2*sizeof(double));
    g=malloc(n/2*sizeof(double));
    n1=n/2;
    e=3.141592653589793/n1;
    for(i=0;i<n1;i++)
    {
       f[i]=x[2*i];
       g[i]=x[2*i+1];
    }
      fft(f,g,n1,1);
      x[0]=f[0]+g[0];
      x[n1]=f[0]-g[0];
      for(i=1;i<n1;i++)
    {
       fr=(f[i]+f[n1-i])/2;
       fi=(g[i]-g[n1-i])/2;
       gr=(g[n1-i]+g[i])/2;
       gi=(f[n1-i]-f[i])/2;
       a=i*e;
       c=cos(a);
       s=sin(a);
       x[i]=fr+c*gr+s*gi;
       x[n-i]=fi+c*gi-s*gr;
    }
    free(f);
    free(g);
}
#endif /* R1FFT_H_ */

4. 例程实现

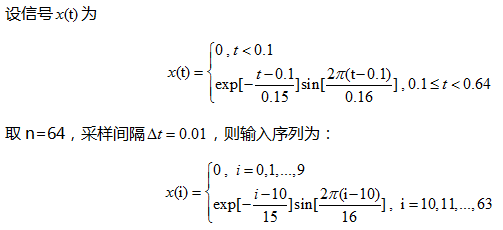
具体实现main.c函数如下：

/*
 * main.c
 *
 *  Created on: 2014年5月27日
 *      Author: lu
 */
#include  <stdio.h> 
#include  <math.h>
#include "r1fft.h"
 
int main(void)
{
    int i,n;
    double x[64];
    FILE *fp;
    n=64;
    for(i=0;i<10;i++) {  x[i]=0; }
    for(i=10;i<n;i++)
    { 
        x[i]=exp(-(i-10)/15.0)*sin(6.2831853*(i-10)/16.0);
    }
    r1fft(x,n);
    printf("\n离散傅立叶变换：\n");
    printf(" %10.7f\t\t",x[0]);
    printf(" \t%10.7f+J %10.7f\n",x[1],x[n-1]);
    for(i=2;i<n/2;i+=2)
    {
       printf("%10.7f+J %10.7f\t",x[i],x[n-i]);
       printf("\t%10.7f+J %10.7f\t",x[i+1],x[n-i-1]);
       printf("\n");
    }
    printf("%10.7f",x[n/2]);
    for(i=1;i<n/2;i++) {  x[i]=sqrt(x[i]*x[i]+x[n-i]*x[n-i]); }
    x[n/2]=fabs(x[n/2]);
    fp=fopen("r1fft.dat","w");
    for(i=0;i<=n/2;i++) { fprintf(fp,"%d\t%f\n",i,x[i]); }
    fclose(fp);
}

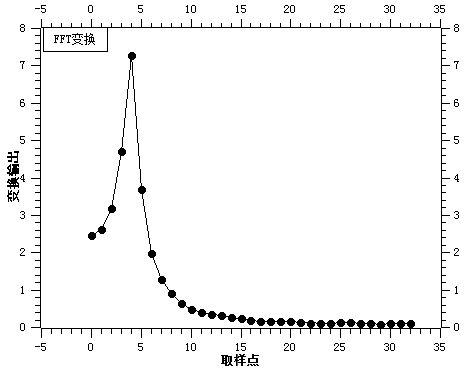
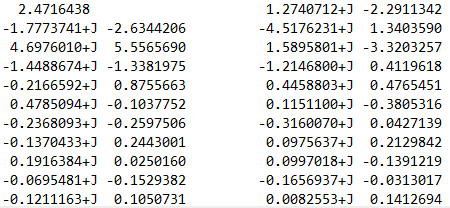
5. 离散傅立叶变换X(k)(k=0,1,..32)

6. 输入序列x(n)的频谱