数据结构(5)—树结构
与线性结构不同,树结构采用的是非线性结构组织数据。在实际应用中,许多问题采用非线性的结构来进行描述会更加简单、方便。
直观地看,树结构是以分支关系定义的一种层次结构。也就是说,应用树结构组织起来的数据应当具有层次关系。具有这类特性的数据在计算机中应用也十分广泛,如:操作系统中的文件管理、网络系统中的域名管理、数据库系统中的索引、编译系统中的语法树等数据都是用树形结构组织的。
1. 树的概念
用形式化的语言描述,树的定义是这样的:树是由n(n≥0)个结点组成的有穷集合。在任意的一颗非空树中:
有且仅有一个称为根(Root)的结点;
当 n>1 时,其余的结点分为 m(m>0) 个互不相交的有限集,T_1, T_2, ...T_M。其中,每一个集合本身又是一颗树,并成为根的子树(SubTree)。
树的结构如下图:


图中该树共有7个结点。其中,A为整个树结构的根结点,即为该树的根;B、C、D 结点为 “根结点 A” 的 “子结点”(child),以B、C、D为根结点又构成3棵树,这3棵树为根结点A的子树(TubTree),其中子树C只有一个根结点。
2. 树结构的存储形式
树结构在计算机中的存储形式很多,这里只介绍最为简单的一种树的存储形式——多重链表表示。在多重链表中,每个结点由一个数据域和若干指针域组成,其中,每一个指针域的指针指向该结点的一个子结点。多种链表的结点类型可描述如下:
#define MAX_CHILD_SZ 10
typedef int elemType_t; ///< 此处以int为例
typedef struct node
{
elemType_t data; ///< 数据域,存放结点信息
struct node *child[MAX_CHILD_SZ]; ///< 子结点指针数组
}binary_node_t; ///< 二叉树结点类型将树的每个结点都定义成如上所示多重链表的结点。其中,data 为结点的数据域,存放结点的信息,child 为指向子结点指针数据,通过这个指针数据将父结点与子结点联系起来。

如上图,是一棵二叉树(每个结点至多有两颗子树的树结构)的内存存储结构。从图中可以看出,每个结点包含一个数据域和两个指针域。数据域用来存放结点中的数据信息,例如:A、B、C 等。指针域用来存放指向子字节的指针,图中 ^ 表示空指针,表明无子结点。
对于二叉树来说,一个结点至多可以有两个子结点,或者一个子结点,或者没有子结点。T 是一个指针,指向二叉树的根结点。
3. 二叉树的定义
本文以二叉树为例进行介绍。
二叉树(Binary Tree)是这样的树结构:它或者为空,或者由一个根结点加上两颗分别称为左子树和右子树的互不相交的二叉树组成。显然,二叉树是递归形式的。
二叉树的一般存储结构采用链式存储结构,直观地讲就是将二叉树的各个结点(根结点、叶子结点等)用链表的形式连接在一起。这样通过特定的算法就可以对二叉树中的每个结点进行操作。
链式存储的二叉树结点内存结构,如下图:


图中,二叉树结点有3个域,其中 lchild 和 rchild 为指针域,用来指向该结点左子结点和右子结点;data 是数据域,用来存放该结点中包含的数据。
二叉树的结点的定义,如下:
typedef int elemType_t; ///< 此处以int为例
typedef struct binary_node_t
{
elemType_t data; ///< 数据域,存放结点信息
struct binary_node_t *lchild, *rchild; ///< 左、右子结点指针数组
}bnode_t; ///< 二叉树结点类型4. 二叉树的遍历
所谓二叉树的遍历,说直白一点就是从二叉树的一个结点(一般为根结点)触发,按照一定的规律访问到该二叉树的全部结点,每个结点只访问一次。这里的 “访问” 依情况而定,它可能是输出结点中的数据,可能是对结点元素进行处理等。
根据二叉树遍历顺序的不同,对二叉树的遍历有3种方案:先序遍历、中序遍历、后续遍历。
4.1 先序遍历
先序遍历二叉树的操作定义为:
(1)访问根结点;
(2)先序遍历左子树;
(3)先序遍历右子树;
/**
* @brief 遍历二叉树
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void pre_order_traverse(bnode_t* T, int level )
{
if(T != NULL)
{
visit(T->data, level); ///< 访问根结点
pre_order_traverse(T->lchild, level + 1); ///< 先序遍历T的左子树
pre_order_traverse(T->rchild, level + 1); ///< 先序遍历T的右子树
}
}4.2 中序遍历
中序遍历二叉树的操作定义为:
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树;
/**
* @brief 遍历二叉树
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void in_order_traverse(bnode_t* T, int level )
{
if(T != NULL)
{
in_order_traverse(T->lchild, level + 1); ///< 中序遍历T的左子树
visit(T->data, level); ///< 访问根结点
in_order_traverse(T->rchild, level + 1); ///< 中序遍历T的右子树
}
}4.3 后序遍历
后序遍历二叉树的操作定义为:
(1)后序遍历左子树;
(2)后续遍历右子树;
(3)访问根结点;
/**
* @brief 遍历二叉树
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void pos_order_traverse(bnode_t* T, int level )
{
if(T != NULL)
{
pos_order_traverse(T->lchild, level + 1); ///< 后序遍历T的左子树
pos_order_traverse(T->rchild, level + 1); ///< 后序遍历T的右子树
visit(T->data, level); ///< 访问根结点
}
}5. 创建二叉树
在已知一颗二叉树的根结点指针的前提下,可以通过二叉树遍历的操作访问二叉树中任何一个结点,求任何一个结点的子结点,求任何一个结点的双亲结点等。同样,通过二叉树的遍历操作也可以生产结点,从而通过二叉树的遍历创建一颗二叉树。
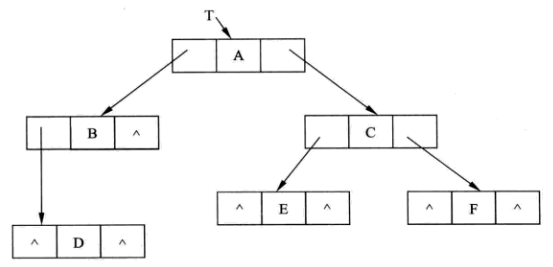
二叉树结构示意图,如下:


该二叉树的先序序列是:A、B、C、D、E、F。如果要按先序序列生成这样一颗二叉树,那么生成结点的次序有应是:A、B、C、D、E、F。
代码实现,如下:
/**
* @brief 创建一颗二叉树
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void create_binary_tree(bnode_t** T)
{
char c;
scanf("%c", &c);
step++;
if(c == '@')
{
printf("步骤%d:子结点赋值NULL\n", step);
*T = NULL;
}
else
{
printf("步骤%d:赋值数据:%c\n",step, c);
*T = (bnode_t*)malloc(sizeof(bnode_t));
(*T)->data = c;
create_binary_tree(&((*T)->lchild));
create_binary_tree(&((*T)->rchild));
}
}6. 示例
#include <stdio.h>
#include <stdlib.h>
typedef int elemType_t; ///< 此处以int为例
static int step = 0; ///< 记录步骤
typedef struct binary_node_t
{
elemType_t data; ///< 数据域,存放结点信息
struct binary_node_t *lchild, *rchild; ///< 左、右子结点指针数组
}bnode_t; ///< 二叉树结点类型
/**
* @brief 创建一颗二叉树
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void create_binary_tree(bnode_t** T)
{
char c;
scanf("%c", &c);
step++;
if(c == '@')
{
printf("步骤%d:子结点赋值NULL\n", step);
*T = NULL;
}
else
{
printf("步骤%d:赋值数据:%c\n",step, c);
*T = (bnode_t*)malloc(sizeof(bnode_t));
(*T)->data = c;
create_binary_tree(&((*T)->lchild));
create_binary_tree(&((*T)->rchild));
}
}
/**
* @brief 访问二叉树,输出字符结点D位于的层数;
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void visit(char c, int level)
{
if(c == 'D')
{
printf("字符 '%c' 所在二叉树的层级为: %d\n", c, level);
}
}
/**
* @brief 遍历二叉树
*
* @param ** T: 二叉树根结点指针
* @return 无
*
*/
void pre_order_traverse(bnode_t* T, int level )
{
if(T != NULL)
{
visit(T->data, level); ///< 访问根结点
pre_order_traverse(T->lchild, level + 1); ///< 先序遍历T的左子树
pre_order_traverse(T->rchild, level + 1); ///< 先序遍历T的右子树
}
}
int main()
{
int level = 1;
bnode_t *T = NULL;
printf("1.请输入二叉树序列(子结点空以'@'标记):");
create_binary_tree(&T);
printf("\n2.测试二叉树的先序遍历:\n");
pre_order_traverse(T,level);
return 0;
}终端输入如下字符:
ABC@@D@@E@F@@
程序执行的步骤,如下图:


示例运行结果如下:


参考来源:
1.《妙趣横生的算法(C语言实现)》 杨峰 编著
