数据结构(6)—图结构
图是一种更为复杂的数据结构。在实际的程序设计中,数据元素之间存在着3种关系:一种是“先行后续”的关系,一个数据元素有一个直接前驱和一个直接后继,这种数据的组织结构叫做线性结构:一种是明显的层次关系,每一层上的数据元素可能和下一层中的多个数据元素(子结点)相关,但只和上一层中的一个数据元素(父结点)相关,这种数据的组织结构叫做树结构;还有一种是数据元素之间存在“一对多”或者“多对一”的关系,也就是任意的两个数据元素之间都可以存在着关系,这种数据的组织结构叫做图结构。
1. 图的概念
图(graph)是由顶点的非空有限集合V(由 N > 0 个顶点组成)与边的集合 E(顶点之间的关系)所构成的。若图 G 中每一条边都没有方向,则称 G 为无向图;若图 G 中每一条边都有方向,则称 G 为有向图。
(1)无向图结构示例,如下:


该无向图由 4 个顶点和 4 条边构成。每个顶点之间都有一条边相连接,而且这些边没有方向。
(2)有向图结构示例,如下:

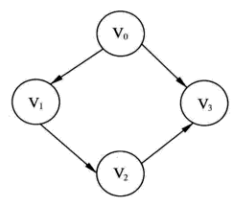
该有向图由 4 个顶点和 4 条边构成。每个顶点之间都有一条边相连接,而且这些边都存在着方向。
2. 图的存储形式
最为常见的图的存储方法有两种:邻接矩阵存储方法 和 邻接表存储方法。
2.1 邻接矩阵存储方法
邻接矩阵存储方法也称数组存储方法,其核心思想是:利用两个数组来存储一个图。这两个数组一个是一维数组,用来存放图中的数据;一个是二维数组,用来表示图中顶点之间的相互关系,称为邻接矩阵。
具体地,一个具有 n 个顶点的图 G,定义一个数组 vertex[0, 1, ..., n-1],将该图中顶点的数据信息分别存放在该数组中对应的数组元素上。例如,顶点 v0 的数据信息存放在 vertex[0] 中,......,顶点 vi 的数据信息存放在 vertex[i] 中。当然数组 vertex 的类型要与图中顶点元素的类型一致。
再定义一个二维数组 A[0...n-1][0...n-1] ,A称为邻接矩阵,它存放顶点之间的关系信息。A[i][j] 定义为:


则前面 <<图2 有向图>>的邻接矩阵可表示为:

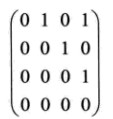
这样通过一个简单的邻接矩阵就可以把一个复杂的图关系表现出来。根据邻接矩阵的信息,可以操作数组 vertex 的元素,从而对整个图进行操作。
2.2 邻接表存储方法
另一种图的存储形式是利用邻接表对图进行存储。邻接矩阵存储方法不适于存储稀疏图(边的数目很少的图),可以用邻接表存储的这类图。
图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法。它由链表和顺序数组组成。链表用来存放边的信息,数组用来存档顶点的数据信息。具体地,对于图中的每一个顶点分别建立一个链表,如果一个图具有 n 个顶点,其邻接表就含有 n 个线性链表。每个链表前面设置一个头结点,称为顶点结点,顶点结点的结构如下:


顶点域 vertex 用来存放顶点的数据信息,指针域 next 指向依附于顶点 vertex 的第一条边。
通常将一个图的 n 个顶点结点放到一个统一的数组中进行管理,并用该数组的下标表示顶点在图中的位置。而在每一个链表中,链表的每一个结点称之为边结点,它表示依附于对应的顶点结点的一条边。边结点的结构如下:


adjvex 域存放该边的另一端顶点在顶点数组中的位置(数组下标);weight 存放边的权重,对于无权重的图,此项省略;next 是指针域,它将第 i 个链表中所有边结点连接成一个链表,最后一个边结点的 next 域为 NULL。
例如,前面 【图2 有向图】 的邻接表表示如下:

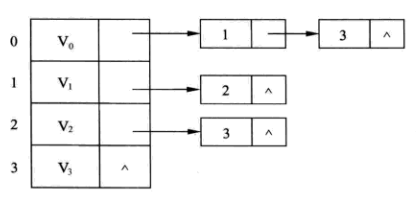
其中顶点 V0 有两条边,其出度(射出的弧的条数)为2,一条边指向顶点 V1, 另一条边指向顶点 V3。而顶点 V3 也有两条边,其出度为0,因此指向的单链表为空。其余的顶点(v1, v2)所指向的单链表也是这样的构成规律。
对于无向图来说,每个顶点指向的单链表就表示附于该顶点边,不考虑边的指向。
例如,前面 【图1 无向图】 的邻接表表示如下:

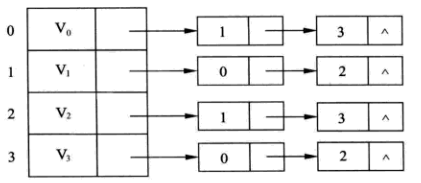
3. 邻接表的定义
根据以上对邻接表结构的介绍,可以通过以下代码定义一个邻接表。
#define MAX_VERTEX_NUM 3
#define vertex_type int
typedef struct arc_node_t
{
int adjvex; ///< 该边指向的顶点所在顺序表的位置
int weight; ///< 边上的权重,可省略
struct arc_node_t *next; ///< 下一边
} a_node_t; ///< 单链表中的结点类型
typedef struct vertex_node_t
{
vertex_type data; ///< 顶点中的数据信息
a_node_t *firstarc; ///< 指向单链表,即指向第一条边
} v_node_t; ///< 顶点类型4. 图的创建
清楚了图的邻接表存储结构,以及如何用代码定义一个邻接表结构,下面就可以应用这些知识创建一个基于邻接表存储结构的图结构。
在创建一个图之前,必须先设计好图的逻辑结构。因为图的创建过程比较复杂,因此建议程序员现在纸上画出要创建的图的逻辑结构,再使用邻接表在计算机中创建出图本身。
例如,应用邻接表创建一个如下图所示的有向图结构。


上图中,该有向图包含3个顶点,内容分别为 0、1、2。不妨设顶点 V0=0;V1=1;V2=2。有了图的逻辑结构,就不难得到该图应用邻接表存储的具体形式。如下:


有了上面这些准备就可以比较容易地创建出图的邻接表存储结构了。
创建一个邻接表存储结构的图的代码描述如下:
/**
* @brief 创建一个邻接表存储结构图
*
* @param n: 要创建的图的顶点个数
* @param *g: 数组指针
* @return 无;
*
*/
void create_graph(int n, v_node_t *g)
{
int i, e;
a_node_t *p, *q;
// 创建图的顶点
printf("步骤1:创建图的顶点: ");
for(i = 0; i < n; i++)
{
printf("%d ", i);
g[i].data = i; // 初始化每个顶点中的数据
g[i].firstarc = NULL; // 初始化第一条边为空
}
// 创建顶点之间的边
printf("\n\n步骤2:创建顶点的边。\n");
for(i = 0; i < n; i++)
{
printf("输入第 %d 顶点的边信息(以 -1 结束):\n", i);
scanf("%d", &e);
while(e != -1)
{
p = (a_node_t *)malloc(sizeof(a_node_t));
p->next = NULL;
p->adjvex = e;
if(g[i].firstarc == NULL)
{
g[i].firstarc = p; // 第一条边
}
else
{
q->next = p; // 下一条边
}
q = p;
scanf("%d", &e);
}
}
}函数 create_graph() 包含两个参数: n 表示要创建的图的顶点的个数; *g 为一个数组指针引用,通过该数据指针修改 v_node_t 类型数组 g 中的内容,从而创建邻接表。
创建一个邻接表的过程分为两个步骤:
(1)首先,先向顶点赋值。赋值顶点的数据g[i].data;且每个顶点的 firstarc 域要初始化为NULL 。
(2)创建顶点之间的边。在创建顶点之间的边时,应当严格按照最开始设计的图的逻辑结构进行边的输入,创建边的过程与创建链表的过程类似。
创建上图的邻接表结构,代码实现如下:
int main()
{
v_node_t G[MAX_VERTEX_NUM]; // 定义图的存储容器
create_graph(3, G); // 创建图
}首先定义 1 个包含 3 个顶点的图,再调用 create_graph() 函数创建该图的邻接表。为方便起见,每个顶点中的数据都自动设为整数,分别为:v0=0;v1=1;v2=2 。这样,顶点 v0=0 存放在 G[0] 中;顶点 v1=1 存放在 G[1] 中;顶点 v2=2 存放在 G[2] 中。
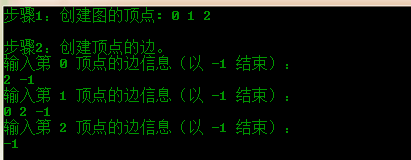
然后,程序提示创建顶点 v0 的边。由于该有向图中顶点 v0 只有一条边射向 v2,而顶点 v2 实际存放在顺序表的 G[2] 中,因此这里输入 2,表示顶点 G[0] 和顶点 G[2] 之前存在一条边;并且以顶点 G[2] 为尾,以顶点 G[0] 为头。再输入-1 表示结束。依次类推。
程序运行结果如下:

5. 图的遍历
5.1 深度优先搜索
同树的遍历一样,图的遍历也是对图的一种最基本的操作。所谓图的遍历就是从图中的某一顶点出发,访遍图中其余顶点,且使每一个顶点只被访问一次。图的遍历操作是求解图的连通性问题,进行拓扑排序,求解最短路径,求解关键路径等运算的基础。
目前普遍应用的图的遍历方法有两种。一种是本节要介绍的深度优先搜索遍历,一种是下一节介绍的广度优先搜索遍历。
深度优先搜索的基本思想是:从图中的某个顶点v出发,访问该顶点 v,然后再依次从 v 的未访问过的邻接点出发,继续深度优先遍历该图,直到图中与顶点 v 路径相通的所有顶点都被访问到为止。由于一个图的结构未必是连通的,因此一次的深度优先搜索不一定可以遍历到图中所有的顶点,若此时仍然有图中的顶点未被访问,就另选图中的一个没有被访问到的顶点作为起始点,继续深度优先搜索。重复上述的操作,直到图中的所有顶点都被访问到为止。显然深度优先搜索的过程是一个递归过程,因为深度优先搜索每次都是重复“访问顶点v,再依次从v的未被访问的邻接点出发继续深度优先搜索”这个操作。
以如下连通图为例:

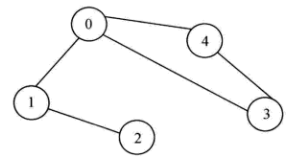
深度优先搜索代码描述如下:
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX_NUM 5
#define vertex_type int
typedef struct arc_node_t
{
int adjvex; ///< 该边指向的顶点所在顺序表的位置
int weight; ///< 边上的权重,可省略
struct arc_node_t *next; ///< 下一边
} a_node_t; ///< 单链表中的结点类型
typedef struct vertex_node_t
{
vertex_type data; ///< 顶点中的数据信息
a_node_t *firstarc; ///< 指向单链表,即指向第一条边
} v_node_t; ///< 顶点类型
int visited[5] = {0,0,0,0,0};
/**
* @brief 创建一个邻接表存储结构图
*
* @param n: 要创建的图的顶点个数
* @param *g: 数组指针
* @return 无;
*
*/
void create_graph(int n, v_node_t *g)
{
int i, e;
a_node_t *p, *q;
// 创建图的顶点
printf("步骤1:创建图的顶点: ");
for(i = 0; i < n; i++)
{
printf("%d ", i);
g[i].data = i; // 初始化每个顶点中的数据
g[i].firstarc = NULL; // 初始化第一条边为空
}
// 创建顶点之间的边
printf("\n\n步骤2:创建顶点的边。\n");
for(i = 0; i < n; i++)
{
printf("输入第 %d 顶点的边信息(以 -1 结束):\n", i);
scanf("%d", &e);
while(e != -1)
{
p = (a_node_t *)malloc(sizeof(a_node_t));
p->next = NULL;
p->adjvex = e;
if(g[i].firstarc == NULL)
{
g[i].firstarc = p; // 第一条边
}
else
{
q->next = p; // 下一条边
}
q = p;
scanf("%d", &e);
}
}
}
/**
* @brief 找到顶点v的第一个临界点
*
* @param v: 顶点
* @param *g: 数组指针
* @return 返回顶点v的第一个邻接点在数组g中的下标
*
*/
int first_adj(v_node_t *g, int v)
{
if(g->firstarc != NULL)
{
return (g[v].firstarc ->adjvex);
}
return -1;
}
/**
* @brief 找到顶点v的下一个临界点
*
* @param v: 顶点
* @param *g: 数组指针
* @return 返回顶点v的下一个邻接点在数组g中的下标
*
*/
int next_adj(v_node_t *g, int v)
{
a_node_t *p;
p = g[v].firstarc;
while(p!=NULL)
{
if(visited[p->adjvex])
{
p = p->next;
}
else
{
return p->adjvex;
}
}
return -1;
}
/**
* @brief 递归进行深度优先搜索
*
* @param v: 顶点
* @param *g: 数组指针
* @return 无;
*
*/
void dfs(v_node_t *g, int v)
{
int w;
printf("%d ",g[v].data);
visited[v] = 1; // 将顶点v对应的访问标记置1
w = first_adj(g,v); // 找到顶点v的第一个邻接点,如果无邻接点,返回-1
while(w != -1)
{
if(visited[w] == 0) // 该顶点未被访问
{
dfs(g,w); // 递归进行深度优先搜索
}
w = next_adj(g,v); // 找到顶点v的下一个邻接点,如果无邻接点,返回-1
}
}
int main()
{
v_node_t G[MAX_VERTEX_NUM]; // 定义图的存储容器
create_graph(5, G); // 创建图
printf("\n步骤3:递归深度优先搜索结果:");
dfs(G, 0);
printf("\n");
}该程序的运行结果如下图:
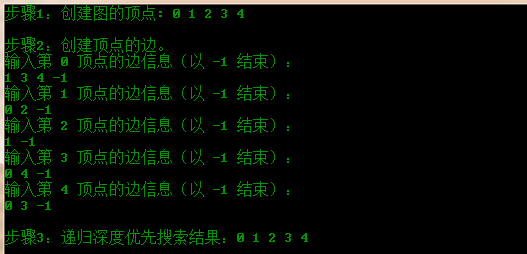

5.2 广度优先搜索
广度优先搜索的基本思想四:从图中的指定顶点 v 出发,先访问顶点 v,然后再依次访问 v 的各个未被访问的邻接点,然后从这些邻接点出发,按照同样的原则依次访问它们的未被访问的邻接点,如此循环,直到图中的所有与 v 相通的邻接点都被访问。与深度优先搜索一样,若此时仍然有图中的顶点未被访问,就另选图中的一个没有被访问到的顶点作为起始点,继续广度优先搜索,直到图中的所有顶点都被访问到为止。
广度优先搜索的思想和深度优先搜索的思想不同。正如它们的名字,深度优先搜索是从一个顶点 v0 开始,按照顺序:访问 v0,深度优先搜索 v0 的第 1 个邻接点,深度优先搜索第 2 个邻接点......深度优先搜索 v0 的第 n 个邻接点。它的特点是:从一点深入下去,深入到不能再深入为止,再从另一点进行深入下去。而广度优先搜索则是一种按层次搜索的方法,即先访问离顶点 v0 最近的顶点 v1、v2、v3...再逐一访问离 v1、v2、v3 ... 最近的点。
以如下连通图为例:
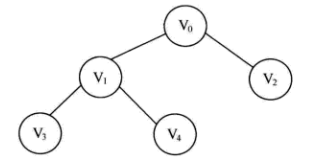

它的执行步骤如下:
访问 v0,
visited[5] = {1,0,0,0,0},并将顶点 v0 入队列,此时队列中只有 v0;将 v0 出队列,求 v0 的第一个邻接点,例如:v1,此时队列为空;
访问 v1,
visited[5] = {1,1,0,0,0},并将顶点 v1 入队列,此时队列只有 v1;调用
next_adj()函数求顶点 v0 的下一个邻接点,得到 v2。由于 v2 未被访问,因此访问 v2,
visited[5] = {1,1,1,0,0},并将顶点 v2 入队列,此时队列中有 v1、v2。调用
next_adj()求顶点 v0 的下一个邻接点,返回 -1。将 v1 出队列,求 v1 的第一个邻接点,例如 v3,此时队列为 v2。
由于 v3 未被访问,因此访问 v3,
visited[5] = {1,1,1,1,0},将顶点 v3 入队列,此时对列中有 v2、v3。用
next_adj()求顶点 v1 的下一个邻接点,得到 v4。由于 v4 未被访问,因此访问 v4,
visited[5] = {1,1,1,1,1},将顶点 v4 入队列,此时对列中有 v2,v3,v4。用
next_adj()求顶点 v1 的下一个邻接点,返回 -1。将 v2 出队列,求 v2 的第一个邻接点,返回 -1,此时对列 v3、v4。
将 v3 出队列,求 v3 的第一个邻接点,返回 -1,此时对列 v4。
将 v4 出队列,求 v4 的第一个邻接点,返回 -1,此时对列空。
参考来源:
1.《妙趣横生的算法(C语言实现)》 杨峰 编著
