a1~an出栈示意图如下:
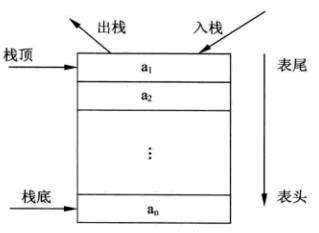

最开始的栈中不包含任何数据,叫做空栈,此时栈顶就是栈底。数据入栈时,从栈顶进入,栈顶栈底分离,整个栈的当前容量变大;数据出栈时,从栈顶弹出,栈底下移,整个栈的当前容量变小。
顺序栈定义如下:
typedef struct
{
elemType_t *base; ///< 指向栈底的指针变量
elemType_t *top; ///< 指向栈顶的指针变量
int stack_size; ///< 指示栈当前可使用的最大容量
}stack_t; ///< 定义一个顺序栈1. 创建一个栈
代码描述如下:
/**
* @brief 创建一个栈空间
*
* @param *s: 所要操作的栈实体
* @return 0-初始化失败;1-初始化成功;
*
*/
int init_stack(stack_t *s)
{
// 内存中开辟一段连续的空间作为栈空间,首地址赋值给 s->base
s->base = (elemType_t*)malloc(STACK_INIT_SIZE * sizeof(elemType_t));
// 分配失败则退出
if(!s->base )
return 0;
// 最开始为空栈,由于没有任何内容,因此栈顶等于栈底
s->top = s->base;
s->stack_size = STACK_INIT_SIZE;
return 1;
}通过以上代码创建一个空栈,其步骤如下描述:
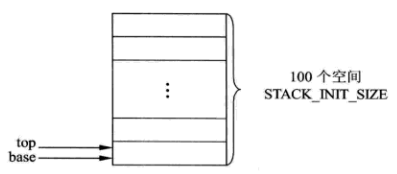
(1)首先通过 malloc() 开辟一段内存空间,大小为预定义的存储空间初始化分配量 STACK_INIT_SIZE 与每个栈元素类型 elemType_t 大小的乘积。将创建的空间的首地址赋值给 s->base ,s 是指向 stack_t 类型变量的指针。
(2)由于最开始栈中没有任何内容,因此是一个空栈,所以栈顶与栈底相同,即 s->top = s->base ;同时,这个新创建的栈的可用空间大小为 STACK_INIT_SIZE 。
该创建好的栈的状态,如下图:

2. 入栈操作
入栈操作也叫压栈操作,就是向栈中存放数据。入栈操作要在栈顶进行,每向栈中压入一个数据,top 指针就增加1,直到栈满为止。
代码描述如下:
/**
* @brief 入栈操作,要在栈顶进行,每向栈中压入一个数据,
* top指针增1,直到栈满。
*
* @param *s: 所要操作的栈实体
* @param e: 入栈的数据内容
* @return 0-入栈失败;1-入栈成功;
*
*/
int push_stack(stack_t *s, elemType_t e)
{
// 栈满,需要追加空间
if((s->top - s->base) >= s->stack_size)
{
printf("ERROR:异常退出!所需栈空间=%d, 最大栈空间=%d\n", (s->top - s->base + 1), s->stack_size);
return 0;
}
// 放入数据
*(s->top) = e;
s->top++;
return 1;
}通过以上代码可以向s指向的栈中,压入一个 elemType_t 类型的数据,具体步骤如下:
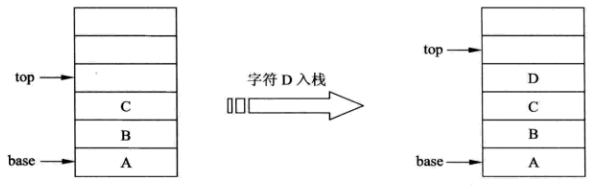
(1)首选判断栈是否已满。 s->top 和 s->base 的差表示该栈的当前实际容量,通过判断此差值是否大于等于 s->stacksize ?若大于等于,则说明该栈已满。此时,可以直接提示异常并退出,也可以使用 realloc() 进行内存的追加。
(2)将待存放到栈中的数据 e 存放到栈顶,然后 top 自加 1,也就是栈顶指针向上移动1。
当不需要追加空间时,其入栈操作示意图如下:

3. 出栈操作
出栈操作就是在栈顶取出数据,栈指针随之向下移动。每当从栈内弹出一个数据,栈的当前容量就减1,可以重复出栈操作,直到该栈变为空栈为止。
代码描述如下:
/**
* @brief 出栈操作
*
* @param *s: 所要操作的栈实体
* @param e: 出栈数据内容
* @return 0-出栈失败;1-出栈成功;
*
*/
int pop_stack(stack_t *s, elemType_t *e)
{
// 若为空栈,则退出
if(s->top == s->base)
{
printf("ERROR:此栈为空栈,无法操作!\n");
return 0;
}
// 得到出栈数据
s->top--;
*e = *(s->top);
return 1;
}通过以上代码可以向s指向的栈中,弹出一个 elemType_t 类型的数据,具体步骤如下:
(1)判断栈顶指针是否与栈底指针相等(s->top == s->base);如果相等,则说明为空栈,异常退出。
(2)先将指针 s->top 减1,再取出指针指向的内容,并赋值给 e。
出栈操作示意图,如下:


4. 其它栈操作
4.1 清空一个栈
清空一个栈,即将栈中的元素全部作废,而栈本身的物理空间并不一定发生改变。因此,只要将 s->top 的内容赋值为 s->base 即可。
代码描述如下:
/**
* @brief 清空一个栈
*
* @param *s: 所要操作的栈实体
* @return 无
*
*/
void clear_stack(stack_t *s)
{
s->top = s->base;
}这样 s->base 等于 s->top,也就表明该栈为空。
4.2 销毁一个栈
销毁一个栈与清空一个栈不同。销毁一个栈需要释放掉该栈所占据的物理内存空间。
代码描述如下:
/**
* @brief 销毁一个栈
*
* @param *s: 所要操作的栈实体
* @return 无
*
*/
void destory_stack(stack_t *s)
{
if(s->stack_size > 0)
{
free(s->base);
}
s->top = NULL;
s->base = s->top;
s->stack_size = 0;
}因此创建一个栈时,使用了 malloc() 在内存的动态去开辟的一段内存空间,因此销毁一个栈需要用 free() 将该空间释放掉;然后,将 s->base 和 s->top 置为 NULL,并将 s->stack_size 置为0。
4.3 计算栈的当前容量
计算栈的当前容量也就是计算栈中元素的个数,因此,只要返回 s.top - s.base 即可。
代码描述如下:
/**
* @brief 计算栈当前容量
*
* @param *s: 所要操作的栈实体
* @return 无
*
*/
int statck_size(stack_t *s)
{
return (s->top - s->base);
}注意:栈的最大容量是指该栈占据内存空间的大小,其值为 s.stack_size ,它与栈的当前容量不是一个概念。
5. 示例
#include <stdio.h>
#include <stdlib.h>
#define STACK_INIT_SIZE (10) //栈大小
#define STACK_INCREMENT_SIZE (9) //压栈大小
#define STACK_DECREMENT_SIZE (5) //出栈大小
typedef int elemType_t; ///< 以int为例
typedef struct
{
elemType_t *base; ///< 指向栈底的指针变量
elemType_t *top; ///< 指向栈顶的指针变量
int stack_size; ///< 指示栈当前可使用的最大容量
}stack_t; ///< 定义一个顺序栈
/**
* @brief 创建一个栈空间
*
* @param *s: 所要操作的栈实体
* @return 0-初始化失败;1-初始化成功;
*
*/
int init_stack(stack_t *s)
{
// 内存中开辟一段连续的空间作为栈空间,首地址赋值给 s->base
s->base = (elemType_t*)malloc(STACK_INIT_SIZE * sizeof(elemType_t));
// 分配失败则退出
if(!s->base )
return 0;
// 最开始为空栈,由于没有任何内容,因此栈顶等于栈底
s->top = s->base;
s->stack_size = STACK_INIT_SIZE;
return 1;
}
/**
* @brief 入栈操作,要在栈顶进行,每向栈中压入一个数据,
* top指针增1,直到栈满。
*
* @param *s: 所要操作的栈实体
* @param e: 入栈的数据内容
* @return 0-入栈失败;1-入栈成功;
*
*/
int push_stack(stack_t *s, elemType_t e)
{
// 栈满,需要追加空间
if((s->top - s->base) >= s->stack_size)
{
printf("ERROR:异常退出!所需栈空间=%d, 最大栈空间=%d\n", (s->top - s->base + 1), s->stack_size);
return 0;
}
// 放入数据
*(s->top) = e;
s->top++;
return 1;
}
/**
* @brief 出栈操作
*
* @param *s: 所要操作的栈实体
* @param e: 出栈数据内容
* @return 0-出栈失败;1-出栈成功;
*
*/
int pop_stack(stack_t *s, elemType_t *e)
{
// 若为空栈,则退出
if(s->top == s->base)
{
printf("ERROR:此栈为空栈,无法操作!\n");
return 0;
}
// 得到出栈数据
s->top--;
*e = *(s->top);
return 1;
}
/**
* @brief 清空一个栈
*
* @param *s: 所要操作的栈实体
* @return 无
*
*/
void clear_stack(stack_t *s)
{
s->top = s->base;
}
/**
* @brief 销毁一个栈
*
* @param *s: 所要操作的栈实体
* @return 无
*
*/
void destory_stack(stack_t *s)
{
if(s->stack_size > 0)
{
free(s->base);
}
s->top = NULL;
s->base = s->top;
s->stack_size = 0;
}
/**
* @brief 计算栈当前容量
*
* @param *s: 所要操作的栈实体
* @return 无
*
*/
int statck_size(stack_t *s)
{
return (s->top - s->base);
}
int main()
{
stack_t stack_main;
elemType_t t_elem;
int i = 0, s_size = 0;
//1.测试创建栈
printf("\n1.创建一个栈:\n");
init_stack(&stack_main);
printf("新栈当前容量为:%d,栈大小为:%d\n", statck_size(&stack_main), stack_main.stack_size);
//2.测试压入栈
printf("\n2.测试压栈:\n");
for(i = 0; i < STACK_INCREMENT_SIZE; i++)
{
t_elem = i + 20;
push_stack(&stack_main, t_elem);
}
// 打印入栈操作后的栈内容,向上生长
printf("--输出当前栈内容--\n");
s_size = statck_size(&stack_main);
for(i = s_size - 1; i >= 0; i--)
{
t_elem = *(stack_main.base + i);
printf("相对栈base位置%d, %d\n", i, t_elem);
}
//3.测试出栈
printf("\n3.测试出栈:\n");
for(i = 0; i < STACK_DECREMENT_SIZE; i++)
{
pop_stack(&stack_main, &t_elem);
printf("出栈位置%d, 出栈数据%d\n", stack_main.top - stack_main.base, t_elem);
}
// 打印出栈操作后的栈内容
printf("--输出当前栈内容--\n");
s_size = statck_size(&stack_main);
for(i = s_size - 1; i >= 0; i--)
{
t_elem = *(stack_main.base + i);
printf("相对栈base位置%d, %d\n", i, t_elem);
}
// 销毁栈
printf("\n3.测试销毁栈:\n");
destory_stack(&stack_main);
s_size = statck_size(&stack_main);
printf("销毁栈成功,栈空间大小为%d\n",s_size);
return 0;
}示例运行结果如下:


参考来源:
1.《妙趣横生的算法(C语言实现)》 杨峰 编著
